How do I buy packs ? It is a good strategy ? When is the next happy hour ? Which packs should I buy ? These are some of the questions that the community ask us everyday. The answers can be found in these particular packs, store and happy hour guide for FIFA 14 Ultimate Team.
Short cut
- Introduction to Packs
It Is Worth to Buy Packs ?
The Packs of FIFA 14 Ultimate Team
The Best Packs to Buy
The Store
Happy Hour
The Best Time to Buy Packs
Season Ticket and Ultimate Edition
FAQ
Introduction to Packs in FIFA 14 Ultimate Team
FUT 14 is a FIFA game mode where we try to get the right cards to build the best team possible. Packs are one of the most important things of this game since
they make possible to introduce the cards in the game. Without them, there would be no cards and without cards FUT 14 would not exist.
All the cards are introduced in FUT 14 through packs by one of the following five methods:
when registering a new team (‘starter pack’);
when returned players access for the first time (‘loyalty packs’);
when purchasing packs in the store;
when winning tournaments or seasons whose prizes are packs;
or when get Daily Gifts and other prizes.
99% of the cards are introduced in the game by the store, when players buy packs. This is what makes this game mode so special for EA Sports. It is a gold mine. Only in FIFA digital sales, which includes Ultimate Team packs, EA has profits higher than $300 million every year. FIFA digital net revenue generated over $145 million in the first half of fiscal 14, an increase of over 25% compared to the first half of fiscal 13.
Follow us in this guide to get to know how, where and when to buy packs.
It Is Worth to Buy Packs ?
This is probably the most common question about FUT 14. The answer depends if the player is using coins or real money to pay.
When a player is building his squad, he needs coins to do it. Some players believe that to use coins to buy packs is the best strategy possible. It isn’t true. We have made several huge tests and our conclusions are very obvious: buying packs with coins is not a good strategy to become richer or to get a better squad. We have opened hundreds of FUT 13 packs, have sold all the cards on the market and the coins we got with the sales were much lower than the coins we spent to buy the packs. The most experienced Ultimate Team players agree with us.
So why are there so many people showing of the fantastic cards they have got in packs ? Maybe because no one likes to show off rubbish and how us useless packs. If only good packs are shared, it gives the idea that all the packs have good cards. Nothing less true.
Many players also think that the only way to be millionaire is buying packs. They find other players on the market that are selling several very expensive cards and they think they got the money buying packs. They don’t. They probably are really good traders or have used scam techniques.
Don’t forget that this is the FIFA core business for EA Sports. Think about it. To sell more packs, they usual do two things:
- They try to give the impression that it is easy to get good cards in packs, using their social networks to show players that got a good card or supporting the most lucky YouTubers that publish videos opening packs with the greatest players;
- They don’t add good cards to packs, forcing players to try their luck again hopping to get the same good cards that other players and youtubers got.
Are you seeing how it works ? Youtubers want to be famous and to be supported by EA Sports, so they produce videos showing how easy is to get good cards in packs. Those who have the luck of getting good cards in packs also want to share it with the world, to show their happiness or simpley to make others jealous. They share it with EA Sports and the company share it with the world. All we see is good cards in packs, so why don’t we do the same. We buy one, two, three, four packs. ‘Maybe in the next one’, we think. Most of the times, players spend part of their coins of a good amount of money and they don’t get a single good card.
If players want to use real money to buy packs, they should know that they will need to spend a good amount of money to get a good squad. We are not saying that it is not a good strategy, we are just saying that it is not a cheap option. For who don’t cares with money, it is a decent decision but we also think that use that money to buy coins it is a safer and less expensive method.
We are not saying to not buy packs any more. It is important that people keep buying packs. First because they are paying the Ultimate Team mode (in the first year it was paid). Then, because the game only works if cards keep being inserted into the game and the only good way to do it is through the store.
Obviously, there are many players that already know that buying packs is not a good strategy. But that doesn’t mean that they give up from buying packs. Why ? First because our brain is always trying to find the path of least resistance and finding ways to give as less effort as possible. Then, because the need of being better, more popular and integrated in a group. This may seems a weird answer but the specialist Gonçalo Cunha explains this very well in THIS fantastic article.
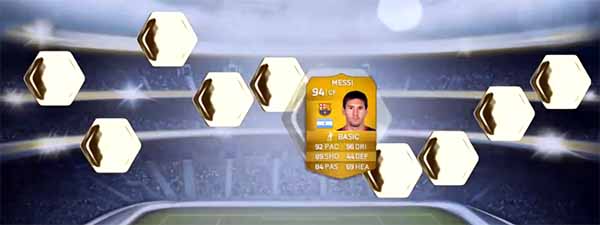
The odds of getting Messi in a pack are like 1 to 60,000 for each card player you open in a pack.
For those who still don’t believe that buying packs is not a good strategy, we will show them with math.
FIFA 14 Ultimate Team has more than 15,000 players. Which player do you want ? Probably the most expensive one, Ronaldo. Let’s see what the odds are of getting him in a pack. First we must know how many players cards have the pack you are opening. Let’s say that you are opening a pack with 4 players. It means that your chances of getting Ronaldo are something like 1 to 3,750, right ? Wrong! There are players with more cards in packs than others.
Cardweight is a metric used to estimate how often a particular card is traded on the FIFA 14 Ultimate Team transfer market. The higher the cardweight number, the higher likely this card is traded on the marketplace. It gives an indication of how rare cards are. The cardweight of Ronaldo is 2, the lower of all game. It means, for example, that he is 100 times less common than David Luiz which cardweight is 200. We know that cardweight does not measure the chance of finding a specific card in a pack since cards that are likely to be kept or quick sold by the original owner will not have an accurate weight. However, through complex calculations we have found a way to find the odds of getting a specific player in a pack using his cardweight, the number of quick sells of that card and the number of cards stored in clubs.
In this case, as Ronaldo is one of that players that when someone buys don’t tries to sell again, the chances of getting him in a pack are 10 times lower than the average of gold players which cardweight is 150. In other words, the chance of getting him are something like 1 to 150,000 for each card player you open in a pack.
What do you think about this ? Do these odds create a good opportunity ? Let’s see. Pick a number between 1 and 150,000 and keep it to yourself. Now, ask someone to try to guess which number you are thinking of. How many times did that person try to guess it ? Thousands, for sure. If you want to know how much money you will have to spend, just multiply the price of each player card in a pack by the number of tries. Now is that a lot of Money ?!
You probably would be happy getting other good players besides Ronaldo. However, all the good cards are very rare. In the top 10 players with best overalls, none have a cardweight higher than 40. For your information, every time someone get a player card in a pack, the odds of getting one of these players are only 1 to 1,400. As you can see, it is very difficult to get good cards in packs.
Final note: if you want fun, choose opening packs. If you want success, avoid them, unless you don’t care to spend real money. In that case, EA Sports will thank you.
The Packs of FIFA 14 Ultimate Team
There are two types of packs: the regular and the special ones. The regular packs are always available on the store. The special packs are available only on specific periods of time, as the Happy Hours. Until now, there are six regular packs and three special packs in FIFA 14 Ultimate Team:
BRONZE PACK
Category: Bronze (Regular)
Cards’ Type: Players, Consumables and Items
Number of Cards: 12
Number of Rare Cards: 1
Price: 400 coins
Great value for increasing club depth. A mix of 12 items, including players, club items and consumables, at least 10 Bronze with 1 rare.
PREMIUM BRONZE PACK
Category: Bronze (Regular)
Cards’ Type: Players, Consumables and Items
Number of Cards: 12
Number of Rare Cards: 3
Price: 750 coins
Triple the rares of a standard bronze pack. A mix of 12 items, including players, club items and consumables, at least 10 Bronze with 3 rare.
SILVER PACK
Category: Silver (Regular)
Cards’ Type: Players and Consumables
Number of Cards: 12
Number of Rare Cards: 1
Price: 2,500 coins or 50 FIFA Points
Great value for building mid-tiered squads. A mix of 12 items, including players, club items and consumables, at least 10 Silver with 1 rare.
PREMIUM SILVER PACK
Category: Silver (Regular)
Cards’ Type: Players and Consumables
Number of Cards: 12
Number of Rare Cards: 3
Price: 3,750 coins or 75 FIFA Points
Triple the rares of a standard silver pack. A mix of 12 items, including players and consumables, at least 10 Silver with 3 rare.
GOLD PACK
Category: Gold (Regular)
Cards’ Type: Players and Consumables
Number of Cards: 12
Number of Rare Cards: 1
Price: 5,000 coins or 100 FIFA Points
Great value for finding top-rate players. A mix of 12 items, including players and consumables, at least 10 Gold with 1 rare.
PREMIUM GOLD PACK
Category: Gold (Regular)
Cards’ Type: Players and Consumables
Number of Cards: 12
Number of Rare Cards: 3
Price: 7,500 coins or 150 FIFA Points
Triple the rares of a standard gold pack. A mix of 12 items, including players and consumables, at least 10 Gold with 3 rare.
SILVER UPGRADE PACK
Category: Special
Cards’ Type: Players
Number of Cards: 12
Number of Rare Cards: –
Price: 15,000 coins or 50 FIFA Points
You one-time chance to upgrade to a silver team. Includes 12 common silver items, with 11 players and 1 manager.
GOLD UPGRADE PACK
Category: Special
Cards’ Type: Players
Number of Cards: 12
Number of Rare Cards: –
Price: 30,000 coins or 75 FIFA Points
You one-time chance to upgrade to a gold team. Includes 12 common gold items, with 11 players and 1 manager.
JUMBO PREMIUM GOLD PACK
Category: Special
Cards’ Type: Players and Consumables
Number of Cards: 24
Number of Rare Cards: 7
Price: 15,000 coins or 300 FIFA Points
Double the size of a premium gold pack with an extra rare. A mix of 24 items, including players and consumables, at least 20 Gold with 7 rares.
PREMIUM GOLD PLAYERS PACK
Category: Special
Cards’ Type: Players
Number of Cards: 12
Number of Rare Cards: 3
Price: 25,000 coins or 350 FIFA Points
Nothing but players to build out your ultimate squads. Includes 12 players, at least 10 gold with 3 rare.
RARE PLAYERS PACK
Category: Special
Cards’ Type: Players
Number of Cards: 12
Number of Rare Cards: 12
Price: 50,000 coins or 1,000 FIFA Points
The most unique top-rated players, all in a single pack. Includes 12 items, all players, all gold, all rare.
JUMBO RARE PLAYERS PACK
Category: Special
Cards’ Type: Players
Number of Cards: 24
Number of Rare Cards: 24
Price: 100,000 coins or 2,000 FIFA Points
The most unique top-rated players, all in a single pack. Includes 24 items, all players, all gold, all rare.
In order to make it easier to compare packs, check out the following table, where you can also see which other packs may be included in the game:
| PRICE | CARDS’ TYPE | NUMBER OF CARDS | |||||
| NAME OF THE PACK | [Coins] | [FP] | Players | Consumables | Items | Total | Rare |
| REGULAR PACKS | |||||||
| Bronze Pack | 400 | Yes | Yes | Yes | 12 | 1 | |
| Premium Bronze Pack | 750 | Yes | Yes | Yes | 12 | 3 | |
| Silver Pack | 2 500 | 50 | Yes | Yes | No | 12 | 1 |
| Premium Silver Pack | 3 750 | 75 | Yes | Yes | No | 12 | 3 |
| Gold Pack (*) | 5 000 | 100 | Yes | Yes | No | 12 | 1 |
| Premium Gold Pack (*) | 7 500 | 150 | Yes | Yes | No | 12 | 3 |
| SPECIAL PACKS | |||||||
| Consumables Pack | 3000 | 50 | No | Yes | No | 12 | 1 |
| Silver Upgrade Pack | 15 000 | 50 | Yes | No | No | 12 | |
| Rare Consumables Pack | 20 000 | 400 | No | Yes | No | 12 | 12 |
| Gold Upgrade Pack | 30 000 | 75 | Yes | No | No | 12 | |
| Jumbo Premium Gold Pack | 15 000 | 300 | Yes | Yes | No | 24 | 7 |
| Prem. Gold Players Pack | 25 000 | 350 | Yes | No | No | 12 | 3 |
| Mega Pack | 35 000 | 700 | Yes | Yes | No | 30 | 18 |
| Rare Players Pack | 50 000 | 1 000 | Yes | No | No | 12 | 12 |
| Jumbo Rare Players Pack | 100 000 | 2 000 | Yes | No | No | 24 | 24 |
| (*) There is also the Gold 13 Pack and the Premium Gold 13 Pack which only difference is having one more non-rare card | |||||||
The Best Packs to Buy
Other question that the community ask us almost every day is ‘which pack to buy’. Obviously it depends of what the player wants. If he wants to build a bronze squad, he should buy a bronze pack. If he wants to get more contracts and other consumables, he should try the consumables packs. However, most of the players want to put their hands in the best and most expensive cards of the game. In that case, they will need to buy Gold packs. But which one ?
Our advice is very simple: purchase the available gold pack with the lowest price per rare player card. These are the only cards that can make some one rich. The other cards are almost worthless. To know which packs have the lowest price per rare card, we only need to divide the price by the number of rare cards. It is easy to do it, following the table above. However, we should pay attention to the category of the pack and if there are other cards besides players. The best packs are the ones with guaranteed rare gold players cards. Into this group, the Premium Gold Players Pack is two times more expensive than the Rare Players Pack or the Jumbo Rare Players Pack. This difference is not so high if we use FIFA Points to pay instead coins. It may be weird but EA Sports doesn’t use a proportional relation between coins and FIFA Points. For example: Jumbo Premium Gold pack and Silver Upgrade pack cost both 15,000 coins but the first one may be purchased with 300 FIFA Points while to the second we only need 50 FIFA Points. Players should also pay attention to this aspect.

Click over the image to learn more about the FIFA Points.
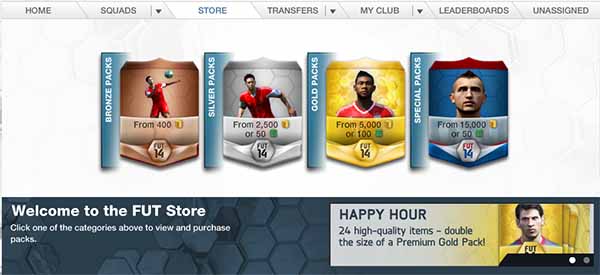
The Store
The store is the place where players can buy packs. They can access to the store through the console or through the FUT Web App.
It is possible to browse in the store until find the right pack. Details of each pack are also provided, including the number of rare cards each pack has.
There are two ways to pay: with coins or with FIFA Points. To know more about FIFA Points, click HERE.

‘My Packs’ can be found on the store and it is where players can claim any packs that they have earned but not yet opened
Happy Hour
There are several misunderstandings about what Happy Hour is and how it works. Some players insist to say that Happy Hour is a period of one hour in which the chances of getting better cards are higher. This is not absolutely true. We will try to clarify those people.
A happy hour is a period of time with special packs available on the store. It may be just one hour but it may also be a full day or even a weekend. Besides the regular packs, in happy hours also exists other packs. They are usually more attractive than the regular ones, because they have a lower cost per rare card. The chances of getting a good card during a happy hour are exactly the same. The only difference is that, most of the times, it will be cheaper to buy packs during Happy Hours.
There are a very rare kind of HH in which the chances of getting a good card are higher. These special Happy Hours are announced as ‘2x Chances’, which means that the chances of getting an IF card during this period are two times higher than usual.
The Happy Hours are not announced in advance. The players may know if there is any Happy Hour in the main page of the FUT Web App or the consoles while it is active, or a few minutes before starting in the Twitter of EA Sports FIFA.
It is impossible to know when will be the next Happy Hour but they are very common in these moments:
– at Wednesdays, between 4pm and 5pm, just before the release of the new TOTW;
– at most of the weekends, usually during large periods of time;
– after a MOTM card release;
– and during the Christmas period (last ten days of December and first two of January).
You can find the Happy Hours’ packs in the special packs section of the store
The Best Time to Buy Packs
As we already have explained, the best times to buy packs are during Happy Hours announced as ‘2x Chance’. It means that the probability of opening a pack with an IF card is twice higher than usually. However, these special Happy Hours are very rare.
Something that should be avoided is to buy packs between 5:30pm and 6pm of Wednesdays because it is impossible to get IF cards in these periods. In other way, it is a good strategy to buy packs during good TOTW weeks or on TOTY/TOTS weeks. In the case of success, the profit will be much higher.
Ultimate Edition and Season Ticket
There are many players confused about what they should do: buying packs on the store, subscribing the Season Ticket or buying the Ultimate Edition. We will try to give a help.
Let’s start by the Ultimate Edition. It is true that the packs purchased on the store are more expensive than the ones that Ultimate Edition offers. However, we strongly recommend to not buy this special edition since it only gives one pack per week. Which means that players need to wait 24 weeks to get all the packs. No one want this.
About the Season Ticket the things are a bit different. As it happens with the Ultimate Edition, subscribers only get one pack per week but it is also true that Season Ticket holders pay 20% less to buy packs on the store with real money (FIFA Points). For who buys many packs, this may be something very useful. The one year subscription gets paid after buying packs that is worth 10k FIFA Points.

Click over the image to learn more about the Season Ticket.
Frequently Asked Questions about Packs, Store and Happy Hour
Q: Should I Invest in Packs ?
A: In our opinion, no. Only if you don’t care about spend real money to get a good team. Learn more about it HERE.
Q: What is the Card weight ?
A: Card weight is a metric used to estimate how often a particular card is traded on the FIFA 14 Ultimate Team transfer market.
Q: Which Packs Should I Buy ?
A: Always look to the available gold packs with the lowest price per rare player card.
Q: Where do I need to go to buy packs ?
A: To the store. You can do it through the console, the FUT Web App or the Companion App.
Q: What is a Happy Hour ?
A: A happy hour is a period of time with special packs available on the store.
Q: It is easier to get better Cards on Happy Hours ?
A: No. Only in the Happy Hours announced as ‘2x Chance’.
Q: When is the next Happy Hour ?
A: Nobody knows. The HH are announced on the console when they start or on EA Sports FIFA Twitter a couple of minutes before.
Q: Should I buy Ultimate Edition or Season Ticket subscription or should I use that money to buy packs ?
A: If you buy packs too often, subscribe the Season Ticket. Otherwise, invest in packs and forget the Ultimate Edition and Season Ticket.












