FIFA 13 Ultimate Team Staff Guide

 
 

Any club that has ambition to achieve the fame, need to have a group of technicians to support players’ work.

This article shows you who is FIFA Ultimate Team Staff, what effect they have on the success of your club and how to choose them.
 

Learn everything about FUT 13 Staff in this complete guide.

 

Short cut

Introduction

Managers

Head Coaches

Goalkeeper Coaches

Fitness Coaches

Physios

FAQ

 
 
 

Introduction to FIFA 13 Ultimate Team Staff

 

In FIFA Ultimate Team, the strengthening of the technical team is made by purchasing staff’s cards. All these cards have the function of amplifying the effect of some consumables.

Here are the categories of FIFA 13 Ultimate Team Staff Cards:

• Managers
• Head Coaches
• Goalkeeper Coaches
• Fitness Coaches
• Physios

 

 

In a very general way, we can say that managers increase the effect of the contract cards and team talk cards, that head coaches increase the effect of the players’ training cards, that goalkeeper coaches increase the effect of the goalkeepers’ training cards, that fitness coaches increase the effect of the fitness cards and that physios increase the effect of the healing cards.

For this reason, it may be a good option to bet on a good and large technical staff when setting up your club.

 
 
 

FIFA 13 Ultimate Team Staff – Managers

 
 

MANAGERS’ ROLE

The manager’s role is the more complex within the staff category. These cards have three basic functions:

• Contribute to the team’s chemistry;
• Increase the players’ morale;
• Help to extend the players’ contracts.

 

Firstly, all teams should have, at least, one manager. He contributes to the team’s chemistry by his nationality and by his favourite formation.

The staff that belongs to a club influences positively the players’ morale and players’ contracts. Each manager’s card shows the percentage gain in morale and the percentage gain in contracts that the manager provides.

By applying a team talk card or a contract card, the effect of these is multiplied by the sum of the managers’ coefficients that the club has. For more managers that you have, the sum of these coefficients can never be greater than 50%. This is valid for both cards: motivational speeches and contracts.

The only manager that needs contracts in order to continue active, is the one who sits on the bench.

 

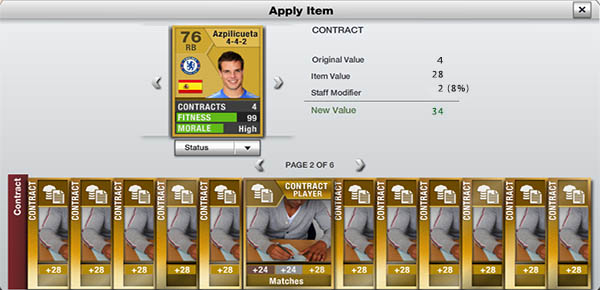
EXAMPLE

The managers contribute to increasing the effect of a contract card or a team talk card with a value ranging between 1 and 3%. This value is written in the manager card, such as nationality, the preferred formation and the number of contracts.

 
 

 

If the staff of your club are the five managers of the image above, you will get a bonus of 8% and 5% when you apply a contract card or a team talk card, respectively. In this case, and following the example of the image below, if you have a gold player with 4 contracts and you apply him a rare gold contract card with 28 contracts, then you will receive a bonus of 2 contracts (4 + 28 x 1.08 = 34). The maths for team talk cards are exactly the same.

 

 

MANAGERS’ CARDS

		MANAGERS’ CARDS
		CONTRACTS	TEAM TALK
GOLD	RARE	3%	0% (2%)
	NORMAL	0%	3%
SILVER	RARE	2%	0% (1%)
	NORMAL	0%	2%
BRONZE	RARE	1%	0% (1%)
	NORMAL	0%	1%

 
There are four rare gold managers, four rare silver managers and four rare bronze managers that are an exception to this rule because they also contribute respectively with 2%, 1% and 1% to the morale of players.
To know the effect that managers have on the team chemistry, please see our Guide to FIFA 13 Ultimate Team Chemistry.

 

MANAGERS LIST

In FIFA 13 Ultimate Team there are 151 managers: 51 bronze, 67 silver and only 33 gold. Check out the full list of managers sorted by their nationality, to make it easier the search for the manager who most contributes to the chemistry of our squad.

 

LIST OF FIFA 13 ULTIMATE TEAM MANAGERS
NAME	NACIONALITY	MORALE	CONTRACTS
Ricardo La Volpe	Argentina	2%
Antonio Mohamed	Argentina	2%
Ruben Omar Romano	Argentina	2%
Tony Popovic	Australia	1%
Ange Postecoglou	Australia	1%
Gary van Egmond	Australia	1%
John Aloisi	Australia	1%
John Kosmina	Australia	1%
Graham Arnold	Australia		1%
Rado Vidošic	Australia		1%
Franz Lederer	Austria	1%
Heimo Pfeifenberger	Austria	1%
Dietmar Kühbauer	Austria		1%
Walter Kogler	Austria	1%
Heinz Fuchsbichler	Austria		1%
Yannick Ferrera	Belgium	1%
Bob Peeters	Belgium	2%
Francky Dury	Belgium	2%
Harm Van Veldhoven	Belgium	2%
Peter Maes	Belgium	2%
Georges Leekens	Belgium		2%
Ariël Jacobs	Belgium		2%
Marc Wilmots	Belgium		3%
Vladimir Petkovic	Bosnia Herzegovina		3%
Ricardo Ferretti	Brazil	2%
Muricy Ramalho	Brazil	3%
Nenad Bjelica	Croatia	1%
Slaven Bilic	Croatia	3%
Michal Bílek	Czech Republic	3%
Lars Søndergaard	Denmark	1%
Johnny Mølby	Denmark		1%
Glen Riddersholm	Denmark	1%	1%
Kent Nielsen	Denmark	2%
Troels Bech	Denmark	2%
Michael Laudrup	Denmark		2%
Steve McClaren	Denmark		2%
Ian Baraclough	England	1%
Ian Crook	England	1%
Terry Butcher	England	1%
Colin Todd	England		1%
Brian McDermott	England	2%
Nigel Adkins	England		2%
Sam Allardyce	England		2%
Steve Clarke	England	1%	2%
Alan Pardew	England	3%
Laurent Roussey	France	1%
Arsène Wenger	France		3%
Peter Hyballa	Germany	2%
Heiko Vogel	Germany	2%
Roger Schmidt	Germany	2%
Joachim Löw	Germany	2%	3%
Vangelis Vlachos	Greece		2%
Sierse Cosmi	Italy		2%
Stefano Colantuono	Italy	3%
Giovanni Trapattoni	Italy		3%
Vincenzo Montella	Italy	3%
Francesco Guidolin	Italy	3%
Luciano Spalletti	Italy		3%
Massimo Carrera	Italy		3%
Roberto Di Matteo	Italy		3%
Massimiliano Allegri	Italy		3%
Roberto Mancini	Italy	2%	3%
Jeff Saibene	Luxemburg	1%
Carlos De Los Cobos	Mexico	2%
Juan Carlos Chávez	Mexico	2%
Enrique Meza	Mexico	2%
Hugo Sánchez	Mexico		2%
Joaquín Del Olmo	Mexico	2%
Benjamín Galindo	Mexico		2%
Guillermo Vázquez	Mexico		2%
Miguel Herrera	Mexico		2%
Víctor Manuel Vucetich	Mexico	2%
José Manuel de la Torre	Mexico	3%
Miodrag Božovic	Montenegro	2%
Art Langeler	Netherlands		1%
Jurgen Streppel	Netherlands		1%
Ton Lokhoff	Netherlands	2%
Jan Wouters	Netherlands	2%
Alex Pastoor	Netherlands	2%
Erwin Koeman	Netherlands	2%
Ruud Brood	Netherlands	2%
Johannes Van’t Schip	Netherlands		2%
Fred Rutten	Netherlands		2%
Marco van Basten	Netherlands		2%
Mario Been	Netherlands		2%
Ron Jans	Netherlands		2%
Ronald Koeman	Netherlands		2%
Gertjan Verbeek	Netherlands		2%
Guus Hiddink	Netherlands	1%	2%
John van den Brom	Netherlands		2%
Dick Advocaat	Netherlands	3%
Frank de Boer	Netherlands	3%
Martin Jol	Netherlands	3%
Ricki Herbert	New Zealand	1%
Declan Devine	Northern Ireland	1%
Steve Lomas	Northern Ireland		1%
Michael O’Neill	Northern Ireland		2%
Neil Lennon	Northern Ireland	1%	2%
Martin O’Neill	Northern Ireland	3%
Brendan Rodgers	Northern Ireland		3%
Jostein Grindhaug	Norway	1%
Dag-Eilev Fagermo	Norway		1%
Kjetil Rekdal	Norway	1%	1%
Åge Hareide	Norway	2%
Ole Gunnar Solskjaer	Norway		2%
João Artur Rosa Alves	Portugal	1%
Jesualdo Ferreira	Portugal		2%
Fernando Santos	Portugal	3%
Andre Villas-Boas	Portugal		3%
Paulo Bento	Portugal		3%
Pat Devlin	Republic of Ireland	1%
Alan Mathews	Republic of Ireland	1%
Mick Cooke	Republic of Ireland	1%
Tommy Dunne	Republic of Ireland	1%
Liam Buckley	Republic of Ireland	1%
Stephen Kenny	Republic of Ireland	1%
Pat Fenlon	Republic of Ireland	1%
Chris Hughton	Republic of Ireland		2%
Gadzhi Gadzhiev	Russia	2%
Vladimir Gazzayev	Russia	2%
Yuri Krasnozhan	Russia	2%
Kurban Berdyev	Russia	3%
Leonid Slutskiy	Russia	3%
Barry Smith	Scotland	1%
Ian Ferguson	Scotland	1%
Craig Brown	Scotland	1%
Derek Adams	Scotland	1%
Danny Lennon	Scotland	1%
Paul Lambert	Scotland	3%
David Moyes	Scotland	3%
Alex Ferguson	Scotland	2%	3%
Roberto Martínez	Spain		2%
Unai Emery	Spain	3%
Vicente Del Bosque	Spain	2%	3%
Magnus Pehrsson	Sweden		1%
Nanne Bergstrand	Sweden		1%
Peter Gerhardsson	Sweden		1%
Kjeil Jonevret	Sweden	1%	1%
Magnus Haglund	Sweden	2%
Jörgen Lennartsson	Sweden	2%
Jan Jönsson	Sweden	2%
Erik Hamrén	Sweden	3%
Bernard Challandes	Switzerland		1%
Uli Forte	Switzerland	1%
Murat Yakin	Switzerland		1%
Marcel Koller	Switzerland	1%	2%
Abdullah Avci	Turkey	3%
Fatih Terim	Turkey	3%
Leonardo Jardim	Venezuela	3%
Mark Hughes	Wales	3%
Tony Pulis	Wales	3%

 

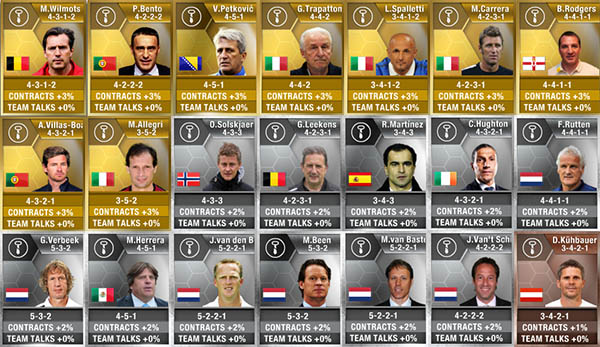
WHICH MANAGERS SHOULD WE BUY ?

The first question that must be asked is: should we buy Managers? For us the answer is yes. In the long run they can make us save many thousands of coins. Especially those that increase the effect of contracts cards. The purchasing of managers is only disapproved for those players who do not think play more than 100 FUT 13 matches. In such cases, the investment in the managers’ cards may be higher than what you earn with them.
The second question is: what managers we should buy? Basically we should buy enough to reach the 50% effect at the lowest possible price, regardless of their nationality, their tactics, their number of contracts or even their level (gold, silver or bronze).
It is here that we need to do math. For this purpose, it makes no sense to buy, for example, Low, Mancini and Del Bosque because the three managers cost several thousand coins that can be used to purchase a greater number of lower-level managers that boost more contracts and moral. For those players who just want to benefit from the 50% contracts bonus, here’s our suggestion, as an example:

 

 

Among these managers we should have one that has the formation of our squad and whose nationality is the same as most players of our team.

 
 
 
 

FIFA 13 Ultimate Team Staff – Head Coaches

 
 

HEAD COACHES’ ROLE

The head coaches are responsible for the development of players’ technical attributes. Each coach’s card shows, in addition to the attribute to which it is engaged, the increment percentage which this coach provides.

By applying a player’s training card, the effect of this is multiplied by the sum of the coaches’ coefficients that the club has. If you can gather all the coach cards of an attribute, when you apply the corresponding training card, this will suffer a 50% bonus.

 

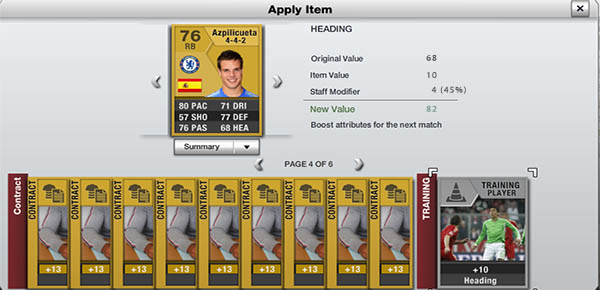
EXAMPLE

The Head Coaches contribute to increasing the effect of a training card with a value ranging between 5 and 15%. This value is written in the head coach card.

 

 

If you have the five head coaches of the image above, you will get a bonus of 45% and 15% when you apply a heading training card or a passing training card, respectively. In this case, and following the example of the image below, if you have a player with heading 68 and you apply him a heading training card +10, then you will receive a bonus of 4 points (68 + 10 x 1.45 = 82). The maths for other attributes training cards are exactly the same.

 

 

HEAD COACHES CARDS

		HEAD COACHES EFFECT
GOLD	RARE	15%
	NORMAL	10%
SILVER	RARE	10%
	NORMAL	5%
BRONZE	RARE	5%
	NORMAL	5%

 

HEAD COACHES LIST

In FIFA 13 Ultimate Team there are 36 head coaches, 12 of each of three levels. Check out the full list of head coaches sorted by the attribute that they boost.

 

LIST OF FIFA 13 ULTIMATE HEAD COACHES
NAME	ATTRIBUTE	BONUS
J Cerny	Heading	15%
P Wadhams	Heading	10%
A Veysey	Heading	10%
J Wang	Heading	5%
D Borrowski	Heading	5%
D Gelsbrecht	Heading	5%
J Maxwell	Defense	15%
G Wellings	Defense	10%
S Kitchen	Defense	10%
H Browse	Defense	5%
M Daish	Defense	5%
H Ekstrom	Defense	5%
G Ivancic	Dribbling	15%
C Smith	Dribbling	10%
M Perrotti	Dribbling	10%
M Inglemarr	Dribbling	5%
C Santiago	Dribbling	5%
S Andersson	Dribbling	5%
S Bodak	Passing	15%
M Rowley	Passing	10%
P Yashin	Passing	10%
J Siggins	Passing	5%
M Gustaffson	Passing	5%
D Doherty	Passing	5%
D Barker	Shooting	15%
N Ustinov	Shooting	10%
P Astin	Shooting	10%
R Archibald	Shooting	5%
L Lorn	Shooting	5%
G Hoffman	Shooting	5%
I Griffith	Pace	15%
P Pannu	Pace	10%
D Pan	Pace	10%
C Facett	Pace	5%
G Pirola	Pace	5%
P Blencowe	Pace	5%

 

WHICH HEAD COACHES SHOULD WE BUY ?

The first question that must be asked is: should we buy Head Coaches? We don’t think so. They only have value to those who use training cards. To use this kind of consumable regularly is too expensive because they expire after one match.
For those gamers that improve the players attributes in the most important times, such as tournaments finals, hire all head coaches for a specific attribute mean a bonus of 50% when applying the corresponding training card. For these players, our advice is to not buy the rare silver cards because their prices are ridiculously expensive for the 10% that they represent.

 
 
 

FIFA 13 Ultimate Team Staff – Goalkeeper Coaches

 

GOALKEEPER COACHES’ ROLE

The goalkeeper coaches are responsible for the development of goalkeepers’ technical attributes. Each goalkeeper coach’s card shows, in addition to the attribute to which it is engaged, the increment percentage which this coach provides.

By applying a goalkeeper’s training card, the effect of this is multiplied by the sum of the goalkeeper coaches’ coefficients that the club has. If you can gather all the goalkeeper coaches’ cards of one attribute, when you apply the corresponding training card, this will suffer a 50% bonus.

 

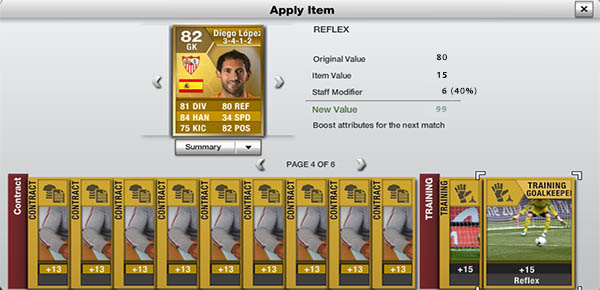
EXAMPLE

The Goalkeeper Coaches contribute to increasing the effect of a training card with a value ranging between 5 and 15%. This value is written in the goalkeeper coach card.

 

 

If you have the five goalkeeper coaches of the image above, you will get a bonus of 40% and 5% when you apply a reflexes training card or a speed training card, respectively. In this case, and following the example of the image below, if you have a goalkeeper with reflexes 80, and you apply him a reflexes training card +15, you will receive a bonus of 6 points (80 + 15 x 1.40 > 99). The maths for other attributes training cards are exactly the same.

 

 

GOALKEEPER COACHES CARDS

		GOALKEEPER COACHES EFFECT
GOLD	RARE	15%
	NORMAL	10%
SILVER	RARE	10%
	NORMAL	5%
BRONZE	RARE	5%
	NORMAL	5%

 

GOALKEEPER COACHES LIST

In FIFA 13 Ultimate Team there are 36 goalkeepers coaches, 12 of each of three levels. Check out the full list of goalkeepers coaches sorted by the attribute that they boost.

 

LIST OF FIFA 13 ULTIMATE TEAM GOALKEEPERS COACHES
NAME	ATTRIBUTE	BONUS
A Rolfe	Handling	15%
D Holme	Handling	10%
B Larsen	Handling	10%
I Japuncic	Handling	5%
D Smith	Handling	5%
M Davis	Handling	5%
T Reid	Diving	15%
M Perry	Diving	10%
A Van Dijk	Diving	10%
G Yuen	Diving	5%
S Subramaniam	Diving	5%
H Mittelstaedt	Diving	5%
S Rempel	Kicking	15%
M Dittmar	Kicking	10%
N Garis	Kicking	10%
E Klammer	Kicking	5%
M Dimpler	Kicking	5%
T Morrison	Kicking	5%
M Leighton	Position	15%
M Sakiani	Position	10%
D Tioseco	Position	10%
D Goetzke	Position	5%
J Tortorello	Position	5%
V Pang	Position	5%
M Ridlen	Reflexes	15%
D Bramall	Reflexes	10%
P Stockdale	Reflexes	10%
G Voros	Reflexes	5%
D Gustafo	Reflexes	5%
V Neville	Reflexes	5%
C Sawatsky	Speed	15%
E Kronner	Speed	10%
S Spinkter	Speed	10%
A Rodrigues	Speed	5%
W Fedranko	Speed	5%
X Parker	Speed	5%

 

WHICH GOALKEEPERS COACHES SHOULD WE BUY ?

The first question that must be asked is: should we buy Goalkeepers Coaches? We don’t think so. They only have value to those who use training cards. To use this kind of consumable regularly is too expensive because they expire after one match.
For those gamers that improve the goalkeepers attributes in the most important times, such as tournaments finals, hire all goalkeepers coaches for a specific attribute mean a bonus of 50% when applying the corresponding training card. For these players, our advice is to not buy the rare silver cards because their prices are too expensive for the 10% that they represent.

 
 
 
 

FIFA 13 Ultimate Team Staff – Fitness Coaches

 

FITNESS COACHES’ ROLE

The role of a fitness coach is to help players to recover the desired physical conditions. Any fitness coach’s card has written the contribution percentage to the player’s physical condition. By applying a fitness card, the number of points that will benefit the player is multiplied by the sum of the coefficients of all the fitness coaches that the club have.

For more fitness coaches that you have, the sum of these coefficients can never be greater than 50%

 

EXAMPLE

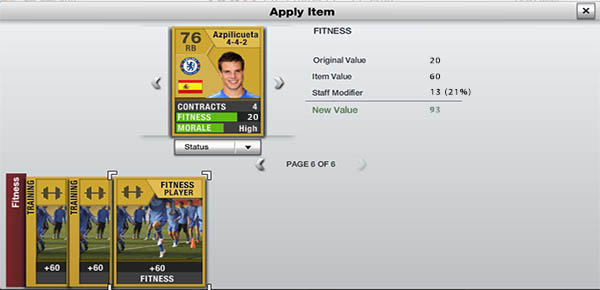
The Fitness Coaches contribute to increasing the effect of a fitness card with a value ranging between 1 and 5%. This value is written in the fitness coach card.

 

 

If you have the five fitness coaches of the image above, you will get a bonus of 21% when you apply a fitness card for the whole squad or just to one player. In this case, and following the example of the image below, if you have a player with fitness 20, and you apply him a fitness card +60, you will receive a bonus of 13 points (20 + 60 x 1.21 = 93).

 

 

FITNESS COACHES CARDS

		FITNESS COACHES EFFECT
	RARE	5%
	NORMAL	3%
SILVER	RARE	3%
	NORMAL	2%
BRONZE	RARE	2%
	NORMAL	1%

 

FITNESS COACHES LIST

In FIFA 13 Ultimate Team there are 36 fitness coaches, 12 of each of three levels. Check out the full list of fitness coaches sorted by their level.

 

LIST OF FIFA 13 ULTIMATE TEAM FITNESS COACHES
NAME	ATTRIBUTE	BONUS
A Neufeld	Gold	5%
D Graff	Gold	5%
E Lee	Gold	5%
J Baerg	Gold	5%
M Arneill	Gold	5%
R Lehman	Gold	5%
A Adams	Gold	3%
F Tsang	Gold	3%
L Sakiani	Gold	3%
S Koo	Gold	3%
S Thomson	Gold	3%
T Shepherd	Gold	3%
C Belle	Silver	3%
C Evans	Silver	3%
D Edmondson	Silver	3%
M Warkentin	Silver	3%
T Dutzi	Silver	3%
T Palmer	Silver	3%
A DaCosta	Silver	2%
B Kuhn	Silver	2%
D Klassen	Silver	2%
F Dickenson	Silver	2%
J Erickson	Silver	2%
J Forsyth	Silver	2%
C Tenhaaf	Bronze	2%
D Sawel	Bronze	2%
D Vanderwolf	Bronze	2%
E Finlay	Bronze	2%
J Bornn	Bronze	2%
S Yeo	Bronze	2%
A Bachman	Bronze	1%
F Baratta	Bronze	1%
L Stewart	Bronze	1%
R Backgaard	Bronze	1%
S Chang	Bronze	1%
T Behl	Bronze	1%

 
 

WHICH FITNESS COACHES SHOULD WE BUY ?

The first question that must be asked is: should we buy Fitness Coaches? We don’t think so. They only have value to those who use fitness cards. To use this kind of consumable regularly is too expensive. Having a squad rotation is a better option. For those who use intensively fitness cards, we recommend the purchase of fitness coaches, especially the gold rare cards because they are best value for money.

 
 
 

FIFA 13 Ultimate Team Staff – Physios

 

PHYSIOS’ ROLE

Owning one or more physios in your club gives you the chance to speed up the recovery of your injured players. Similarly to the head coaches and the players’ training cards, to the goalkeeper coaches and the goalkeepers’ training cards, and to the fitness coaches and the fitness cards, physios also increase the effect of healing cards.

By applying a healing card, the effect of this is multiplied by the sum of all the physios’ coefficients specialists in that injury that your club own.

If you can gather all the physios’ cards of an injury, when you apply the corresponding healing card, this will suffer a 50% bonus.

 

EXAMPLE

The Physios contribute to increasing the effect of a healing card with a value ranging between 5 and 15%. This value is written in the physio card.

 

 

If you have the five physios of the image above, you will get a bonus of 40% and 5% when you apply a back healing card or a foot healing card, respectively. In this case, if you have a injury player on the back out for 4 matches, and you apply him a healing card +2 for all injuries, the player will be out only for one match (4 – 2 x 1,40 = 1).

 

PHYSIOS CARDS

		PHYSIOS EFFECT
GOLD	RARE	15%
	NORMAL	10%
SILVER	RARE	10%
	NORMAL	5%
BRONZE	RARE	5%
	NORMAL	5%

 

PHYSIOS LIST

In FIFA 13 Ultimate Team there are 42 physios, six of each of seven injuries. Check out the full list of physios sorted by the injuries.

 

LIST OF FIFA 13 ULTIMATE TEAM PHYSIOS
NAME	INJURY	BONUS
S Slanski	Arm	15%
V Jackson	Arm	10%
P Newbury	Arm	10%
E Cho	Arm	5%
J Bradford	Arm	5%
D Collomb	Arm	5%
L De Goosman	Head	15%
J Newton	Head	10%
M Pressley	Head	10%
A Outing	Head	5%
C Bailey	Head	5%
J Farr	Head	5%
D Schneider	Back	15%
A Bowden	Back	10%
M Chen	Back	10%
Y Santos	Back	5%
I Yeung	Back	5%
D Yoo	Back	5%
M Cree	Knee	15%
J McCarthy	Knee	10%
P Beetham	Knee	10%
S Bissel	Knee	5%
L Hazell	Knee	5%
N Pandev	Knee	5%
D Crowe	Shoulder	15%
C McKee	Shoulder	10%
A Patient	Shoulder	10%
L Carluccio	Shoulder	5%
C Berry	Shoulder	5%
P Jones	Shoulder	5%
T Lee	Foot	15%
J Kalinski	Foot	10%
S Pang	Foot	10%
Y Tomas	Foot	5%
C Ramsey	Foot	5%
S Parkin	Foot	5%
D Adamson	Leg	15%
B Kilford	Leg	10%
M Hood	Leg	10%
H Dent	Leg	5%
R Fletcher	Leg	5%
S Gardner	Leg	5%

 
 

WHICH PHYSIOS SHOULD WE BUY ?

The first question that must be asked is: should we buy Physios? We don’t think so. They only have value to those who use healing cards. To use this kind of consumable regularly is too expensive. Having a squad rotation is a better option.
For those who use intensively healing cards, we recommend the purchase of physios, especially the gold rare cards because they are best value for money.

 
 
 

FIFA 13 Ultimate Team Staff – Frequently Asked Questions (FAQ)

 
Q: How many staff’s can I own on my club ?
A: The only limit is that you can’t have a duplicate card.
 
Q: What should I do in order to staff make effect ?
A: Nothing. You just need to hire them and store them on your club.
 
Q: There is any limit to the staff effect ?
A: Yes. Usually 50%.
 
Q: Where can I see how my staff affect training and development cards ?
A: You can go to Active Squad – Actions Player – Consumables and then select the consumable card which you want to know the staff effect.
 
Q: How can I buy Staff ?
A: In the auction house, using the filter staff, or in packs.
 
Q: Where can I find the staff that I hired ?
A: In My Club.
 
Q: What is the difference of having a gold manager or a bronze manager ?
A: To the chemistry, gold managers are more valuable than silver and silver than bronze. The other difference is about the contract and team talk percentage boost.
 
Q: Can I change the formation of my manager ?
A: Yes. You just need to apply him a formation manager card that you can find in packs or in auction house (filter: training).
 
Q: Which staff spends contracts ?
A: Only the managers that sit on the bench. All the others that are stored on the club produce their effect without spending contracts.
 
Q: Can I choose to have no staff at my club ?
A: Yes. Although it is highly recommended to have at least one manager to put on the bench.